Subsonic Outflow Condition in Quasi 1-D nozzle flow

準1次元ノズルフローを亜音速流出条件で解きます。

はじめに

前々回と前回ではいずれも超音速で流出する流れを取り扱った。 しかし出口圧力の設定次第では、流れは超音速にならずに亜音速のままノズルから出ていくケースも起こりうる。 この記事ではそうしたケースを計算で取り扱う。

支配方程式

これまでと変わらないので省略。

問題設定

出口圧力比と対応するノズル流れ

あとで追記するかも。

ノズル形状

亜音速流れに対してはノズル断面積$A$が以下の式で与えられるノズルを取り扱う。

$x = 1.5$に向かってすぼまっていくが、$x = 1.5$以降はそんなに拡がらない。

初期条件

文献 ^[1] の式 (7.90a)-(7.90c) で与えられる値を用いた。 文献いわく

for the initial conditions, let us somewhat arbitrarily set up the following variations: (p. 330)

とあり、わりと任意性がある様子。

境界条件

流入側は亜音速流入なのでこれまでと変わらない。

流出側は亜音速流出 (subsonic outflow) であることから、特性線2本のうち1本は（速さ$a-v$で）計算領域に入ってきて、もう1本は（速さ$a+v$で）計算領域から出ていく。 また流れは計算領域より出ていく。 このことより1変数を固定し、2変数を変動させる。 固定する変数としては、今回の問題設定からは圧力（圧力比）$p_e/p_0$が道理であるのでそのようにする。

ノズル内流れの計算コードを参考に、原始変数に境界条件を与え、保存変数は原始変数より従属的に求めるようにする。

# primitive variables
rc[N] = 2.0 * rc[N-1] - rc[N-2]   # extrapolation
uc[N] = 2.0 * uc[N-1] - uc[N-2]   # extrapolation
pc[N] = PEP0                      # fixed
tc[N] = pc[N] / rc[N]             # dependent
cc[N] = T0 * sqrt(pc[N] / rc[N])  # dependent

# conservative variables
q[1,N] = rc[N] * a[N]
q[2,N] = rc[N] * uc[N] * a[N]
q[3,N] = rc[N] * (tc[N] / (gamma - 1.0) + 0.5 * gamma * uc[N]^2) * a[N]

結果

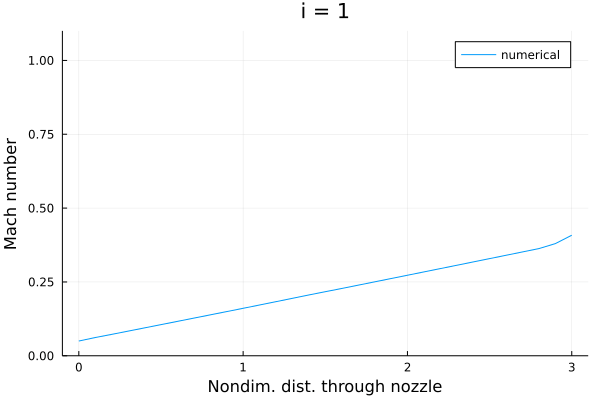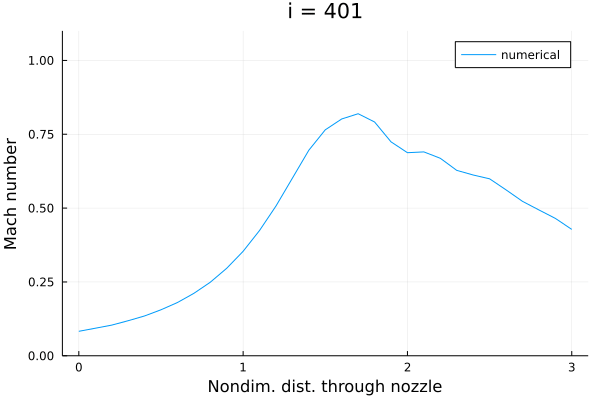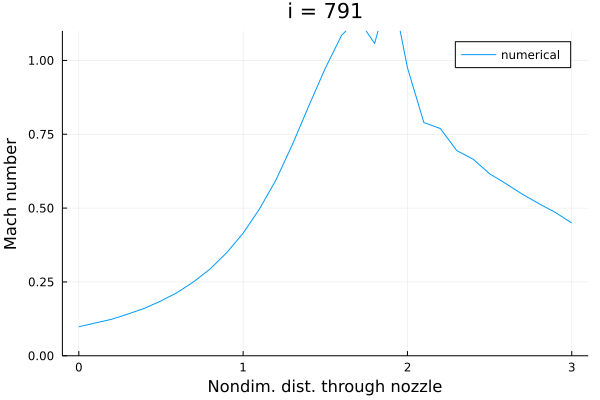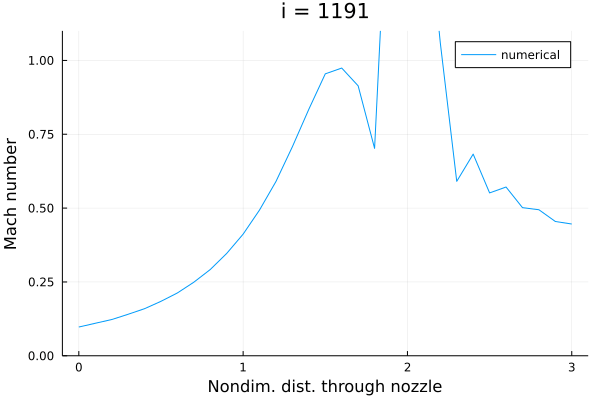
圧力比$p_e/p_0 = 0.93$を与えた場合のマッハ数分布の収束過程。

文献にあったように4000ステップくらい回さないと収束しなくて、超音速流出条件よりも収束性が悪い。 理由として考えているところ:

• 境界条件として変数を固定することの拘束が強い（固定端みたくなってる）

• 文献 ^[2] いわく「最大固有値に合わせて時間刻み幅を設定すると、最大でない固有値に対応する固有ベクトルの成分の成長が遅くなる (p. 151)」今回は超音速流出のケースよりも低速なので成長が遅くなっている

圧力比$p_e/p_0 = 0.85$を与えた場合には流れ場の状況が厳しくなって発散する:

ちなみにこれまで通りの超音速流出条件を与えると、流れ場は超音速流れの解析解に一致する:

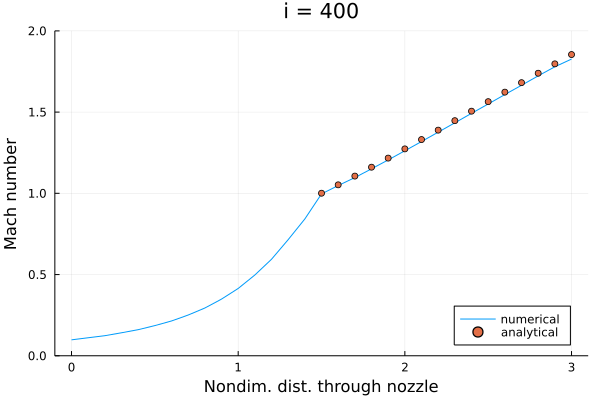
実際に実験室でこの流れを再現するためには、何らかの出口圧力を与えてリザーバーからノズルへと流れを駆動してやる必要がある。 亜音速のケースでは出口圧力（圧力比）を与えるのでいいとして、超音速のケースでは出口圧力は与える必要がなく、計算の結果として求まるというのがちょっと直感的でないな、という感想だった。 コードの中では全く同じ計算をしているので、単に境界条件の違いということになる。 解析においては内点での計算スキームにばかり目が行きがちだけど、境界条件にももっと注意深くなりたいし、うまくなりたい。