Conservation form in Quasi 1-D nozzle flow

準1次元ノズルフローを保存型で解きます。

はじめに
問題設定
支配方程式
保存型表示
離散化
その他、数値解析に必要な諸々
1. 初期条件
2. 境界条件
結果
おわりに

はじめに

前回のthe first echelonでは準1次元ノズルフローを変数 $\rho$ , $V$ , $T$ に対して解いた。解いている変数がいつもの保存変数になっていなかったことについて、文献 ^[1] で続く7.5節では保存型で定式化した解法が示されている。この節にならって、同じ問題を今度は保存変数を使って解くことを試みる。

問題設定

前回の記事では書き忘れていたけど、断面積 $A$ が以下の式で与えられるノズルに対して流れを解いているのであった。

A = 1 + 2.2(x-1.5)^2 \qquad 0 \leq x \leq 3

計算領域は $0 \leq x \leq 3$ であり、 $x = 1.5$ の位置で最小値 $A=1$ を取る。

支配方程式

密度 $\rho$ 、運動量 $\rho V$ 、全エネルギー $\rho (e + V^2 / 2)$ に対する式をそれぞれ得る。（導出は割愛）

準1次元問題として解いているため、各項には断面積が掛けられていることに注意。

密度:

\frac{\partial \rho A}{\partial t} + \frac{\partial \rho A V}{\partial x} = 0

運動量:

\frac{\partial \rho A V}{\partial t} + \frac{\partial \rho A V^2 + (1 / \gamma) p A}{\partial x} = \frac{1}{\gamma} p \frac{\partial A}{\partial x}

右辺の圧力項は断面積変化がなければゼロとなる。

全エネルギー:

\frac{\partial \rho (\frac{e}{\gamma - 1} + \frac{\gamma}{2}V^2)A}{\partial t} + \frac{\partial \rho (\frac{e}{\gamma - 1} + \frac{\gamma}{2}V^2) V A + p A V}{\partial x} = 0

ここで、新たに導入した変数 $e$ は単位体積あたりの全エネルギーではなく単位質量あたりの内部エネルギーであるので注意。また変数はいずれも無次元化しているが、 $p$ と $e$ についてはいずれも $\rho_0 a_0^2$ ではなくリザーバーでの値 $p_0$ と $e_0$ をそれぞれ用いて無次元化していることに注意。

保存型表示

前節での保存量に対して以下の保存変数を導入する。

U_1 = \rho A

U_2 = \rho A V

U_3 = \rho (\frac{e}{\gamma - 1} + \frac{\gamma}{2}V^2)A

また、支配方程式中の流束を以下のようにおく。

F_1 = \rho A V

F_2 = \rho A V^2 + \frac{1}{\gamma} p A

F_3 = \rho (\frac{e}{\gamma - 1} + \frac{\gamma}{2}V^2) V A + p A V

J_2 = \frac{1}{\gamma} p \frac{\partial A}{\partial x}

これらの項は保存量 $U_1$ , $U_2$ , $U_3$ で表すことができて、

F_1 = U_2

F_2 = \frac{U_2^2}{U_1} + \frac{\gamma - 1}{\gamma}(U_3 - \frac{\gamma}{2}\frac{U_2^2}{U_1})

F_3 = \gamma \frac{U_2 U_3}{U_1} - \frac{\gamma (\gamma - 1)}{2} \frac{U_2^3}{U_1^2}

J_2 = \frac{\gamma - 1}{\gamma} (U_3 - \frac{\gamma}{2} \frac{U_2^2}{U_1}) \frac{\partial (\ln{A})}{\partial x}

このように流束はすべて保存変数を使って計算することを考える。ここまで徹底して保存変数に置き換えるやり方は見たことがなかったので参考になった。

ただし文献 ^[1] で示されている通り、実際の解法では $J_2$ は式 (11) の形のまま扱っていて、 $p = \rho T$ の関係より圧力の代わりに密度と温度を使って解いている。

離散化

前回と同様にMacCormack法を用いる。

ただし何も考えずに実装したら配列の添字の領域外参照が発生したので、少しだけ細工した。（あとでソースコードで示したい）

その他、数値解析に必要な諸々

時間刻みは前回と同様なので省略。

初期条件

文献 ^[1] の式 (7.120a)-(7.120f) で与えられる値を用いた。前回の初期条件よりも手の込んだ分布になっているが、文献いわく

this is in anticipation that the stability behavior of the finite-difference formulation using the conservation form of the governing equation might be slightly more sensitive, and therefore it is useful to start with more improved initial conditions than those given in Sec. 7.3.1 by Eqs. (7.74a) to (7.74c). (p.344)

とのこと。安定性についての言及がもし本当ならばこれは残念。

流入境界は亜音速流れなので2変数を固定し1変数を変動させる。ここで固定しているのは保存変数ではなくて原始変数 (primitive variables)、それも前回と同様に密度 $\rho$ と温度 $T$ になっている。それに対して、前回と同様に変動させている（＝外挿で求めている）のは速度 $V$ ではなく、保存変数 $U_2$ になっている。外挿した保存変数 $U_2$ からは（密度一定なので）速度が求まり、速度が得られればもう一つの保存変数 $U_3$ の値も（温度一定なので）求まる。結果的に（もっとも）筋の良いやり方になっているように見えるけれども、このあたりのどの変数を固定し・どれを動かすべきかの相場観はまだ掴めていない。

流出境界は超音速流れなので3つの保存変数 $U_1$ , $U_2$ , $U_3$ を変動させる。これは楽。

結果

前回と同様にマッハ数分布。 JuliaでGIFアニメーションを作れるようになったので動画にしてみる。

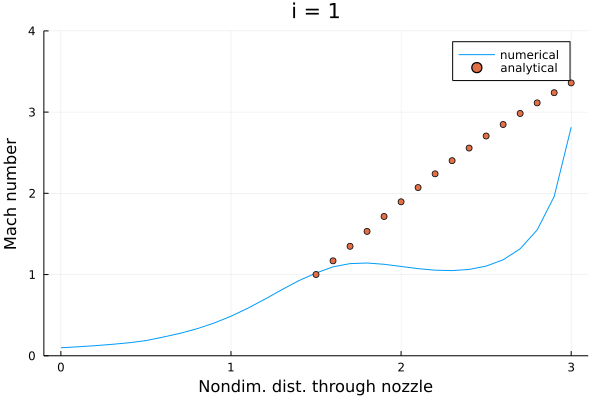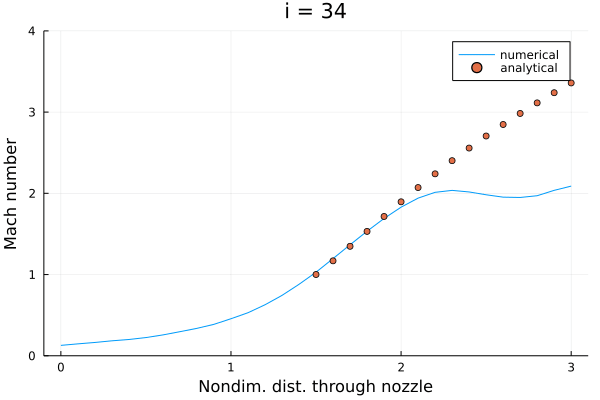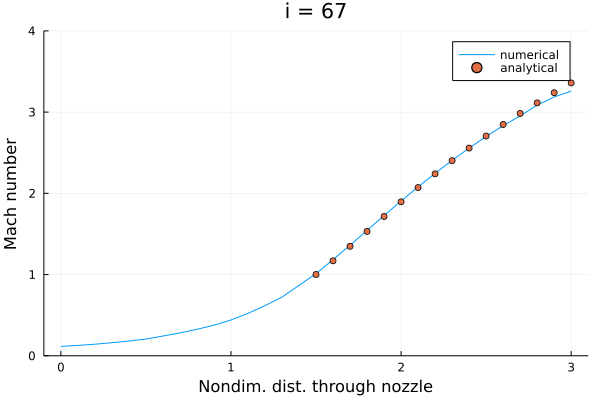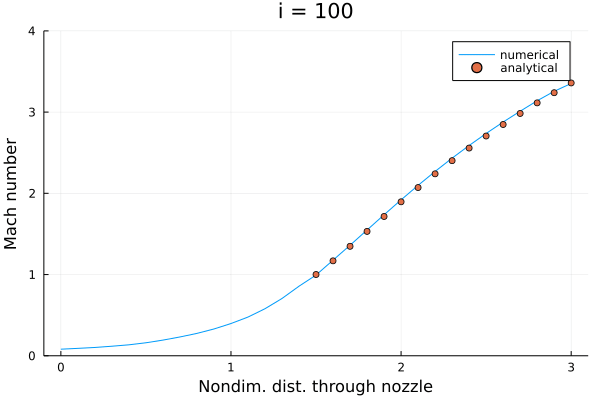
100ステップ動かすとだいたい解析解に近づく。実際にはもう少しステップ数を稼いで収束させたほうが良さそう。

初期条件のところで述べたように、今回は "改善された (improved)" 初期条件が与えられていた。上のアニメーションからもわかるように、とりわけ亜音速領域 ( $x < 1.5$ ) では少し変動しただけで収束解が得られていて、あまり面白みがない。懸念された安定性の確認も兼ねて、もっと雑な初期条件を与えてみた。

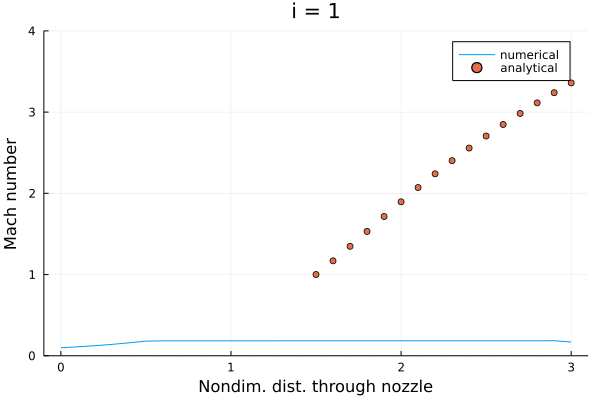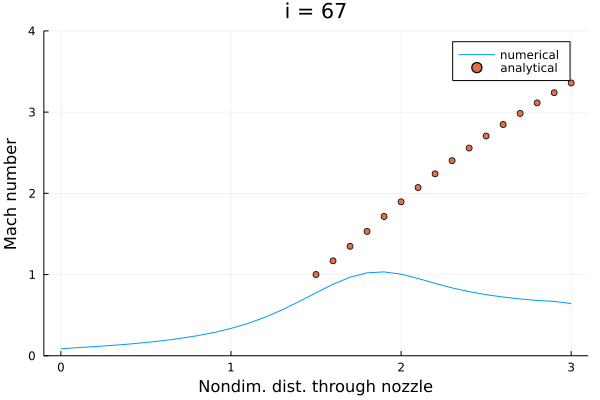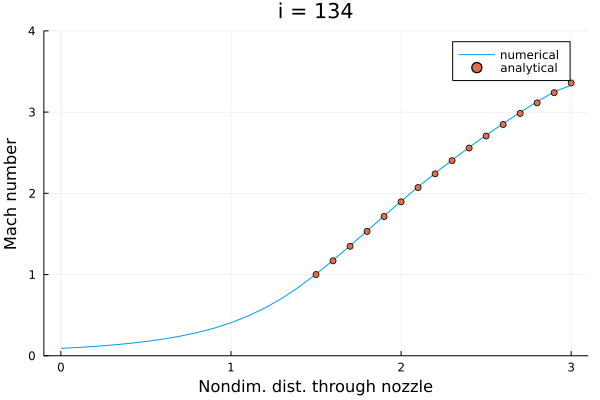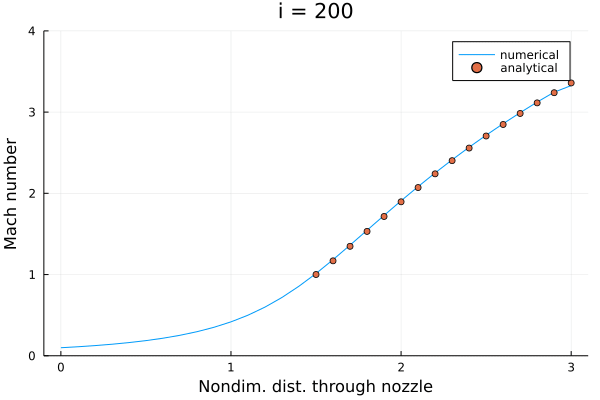
一応解くことができたので一安心。

ステップ数 $i=40$ 付近では流入直後の位置でマッハ数がゼロを下回っている。このステップでの物理量を確認したところ、速度が負の値になっていた。本来であればノズルフローにおいては（ $p_0 \gt p_{exit}$ である限り）逆流は起こりえず、非物理的な状態ではあったものの、なんとか持ちこたえてくれた。

おわりに

準1次元ノズルフローを保存型で解いて、前回の非保存型で解いた場合と同様の解を得ることができた。

今回の保存型の定式化は文献 ^[1] に準じたものだったけど、しかし普段よく見かける式とは少し異なる部分があった: $e$ が内部エネルギーであること、また圧力とエネルギーが参照値で無次元化されていること。次はこの2点を修正して見慣れた式に置き換えることを試みたい。

[1]	John D. Anderson, "Computational Fluid Dynamics: The Basics With Applications," McGraw-Hill Inc. (1995)

monotonica Engimono Notebook and more