Quasi 1-D nozzle flow as the first echelon

準1次元ノズルフローをシミュレーションで解きます。

問題設定
支配方程式
離散化
その他、数値解析に必要な諸々
1. 時間刻み
2. 境界条件
結果
おわりに

問題設定

等エントロピー流れとしてよく見かけるノズルフローを準1次元的に解く。本来は2次元（あるいは3次元）的な流れ場であるものの、いくつかの仮定を置くことで1次元の流れとみなす。すなわち:

断面内の物理量は一定とする
流れに垂直な速度成分を0とする

ノズルフローはおもに風洞などで見ることができて、少し調べた感じではNASAの風洞設計の資料 (Wind Tunnel Design)が概要をつかむのに良さそう。亜音速 (subsonic) の風洞であればcontractionのすぐ後ろにtest sectionを設ける。一方で超音速 (supersonic) の風洞であれば、contractionからさらにdiffuserを経てtest sectionへと至る。この違いはマッハ数 $Ma=1$ をはさんで気体の性質が変化することに由来している。

自転車乗りの論文をかつて読んだときFig. 5に風洞の模式図があった。この風洞がつくる流れは亜音速であり、図中央付近のcontractionからのnozzle exitを経た直後にtest sectionが設けられていることがわかる。

古き良き文献 ^[1] においては第7章でこの問題が取り上げられている。支配方程式、離散化、数値解析の諸々で3つのechelon ^[2] が構成されていることから、この記事でもそうした段階に基づいてシミュレーションの全体像を眺めていくことにする。

支配方程式

連続の式より密度 $\rho$ 、運動量保存則より速度 $V$ 、エネルギー保存則より温度 $T$ の式をそれぞれ得る。（導出は割愛）

密度:

\frac{\partial \rho}{\partial t}=-\rho \frac{\partial V}{\partial x}-\rho V \frac{\partial(\ln{A})}{\partial x}-V\frac{\partial \rho}{\partial x}

速度:

\frac{\partial V}{\partial t}=-V \frac{\partial V}{\partial x}-\frac{1}{\gamma}(\frac{\partial T}{\partial x}+\frac{T}{\rho}\frac{\partial \rho}{\partial x})

温度:

\frac{\partial T}{\partial t}=-V \frac{\partial T}{\partial x}-(\gamma - 1)T\{\frac{\partial V}{\partial x}+V\frac{\partial (\ln{A})}{\partial x}\}

変数はいずれも無次元化している。無次元化にはリザーバーでの温度 $T_0$ 、密度 $\rho_0$ 、音速 $a_0$ を用いる。

解いている変数がいつもの保存変数になっていないが、これは文献 ^[1] のこのあとに続く節で種明かしがあった。続く記事でも触れられればと思う。

離散化

空間の離散化には後退差分ではなくMacCormack法を使う。 MacCormack法は時空間の双方で2次精度である（文献 ^[1] のp. 222）。

離散化式は省略。（あとでソースコードで示したい）

その他、数値解析に必要な諸々

時間刻み

時間刻み $\Delta t$ は任意のCFL数 $C$ （ここでは $C = 0.5$ ）を与えることで以下の式で定める:

\Delta t = C \frac{\Delta x}{a + V}

移流方程式のCFL数の式 $C = c \Delta t / \Delta x$ （文献 ^[1] の式 (4.84)）と類似しているが、移流速度が $a + V$ に変わっている。これは特性線の（最大）速度が $a + V$ であるため（たぶん）。

また、実際には音速 $a$ と速度 $V$ がいずれも変数であることから、前式で与えられる時間刻みはセル毎に異なる:

\Delta t_i = C \frac{\Delta x}{a_i + V_i} \qquad (i = 1, 2, ..., N)

セル毎に異なる時間刻みを用いるか、それともセル全体で統一するかには選択の余地がある。文献では後者を選択している。この実装に一手間かかった。

境界条件

これまでちゃんと知らなかった話だったので、ためになった。特性理論からこのようになる様子。

亜音速流入 (subsonic inflow)
- 2変数（密度、温度）を固定
- 1変数（速度）を変動させる
超音速流出 (supersonic outflow)
- 3変数（密度、温度、速度）を変動させる

変動させる場合にはいずれも線形外挿を用いる。

結果

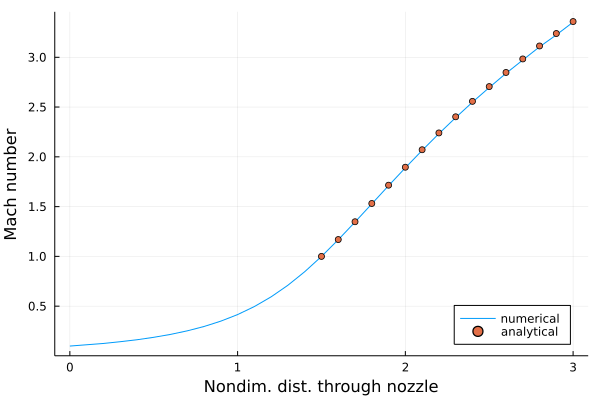
文献での例と同様に1400ステップ回したときのマッハ数分布。横軸に流れ方向位置、縦軸にマッハ数をとっていて、とりあえず解析解に一致する結果を得ることができた。 JuliaのPlots (GR) でプロットしている。

以下ははまりポイント:

最後に収束解が得られれば時間精度はいらないと思って、MacCormack法ではなく空間1次後退差分でやったら計算が発散した。2次中心でもまあ発散するよねという感じでうまくいかない。どこが悪いのかわからなかったので、結局1ステップ実行後の結果が一致するところまで検証を追い込む必要があった。
- 文献 ^[1] ではとても丁寧なことに、1ステップ実行後の結果が詳細に記述されている。はじめはここまではいらないだろうと思ったものの、おかげで助けられた。
- MacCormack法は単に精度向上だけではなく、計算の安定性にも寄与していると考えられる。
Juliaの継続行の解釈ではまった。以下のコードでは所望の結果が得られないということに気付くまでに時間を要した。
- 今のところうまい解決策を思い当たっていないけど、とりあえず括弧で全部くくることで回避している。

drdt = - r[i] * ((u[i+1] - u[i]) / dx)
     - r[i] * u[i] * ((log(a[i+1]) - log(a[i])) / dx)
     - u[i] * ((r[i+1] - r[i]) / dx)

drdt = (
     - r[i] * ((u[i+1] - u[i]) / dx)
     - r[i] * u[i] * ((log(a[i+1]) - log(a[i])) / dx)
     - u[i] * ((r[i+1] - r[i]) / dx)
)

断面積比が与えられたときのマッハ数は以下の式から求まる…はずだが、この式を解くのはそう単純でないことに気付いた。文献 ^[1] には陰解法で解けるとだけ書いてあって、具体的な解法は示されていない。調べたらNASAのサイト (Area Ratio)に計算スクリプトが用意されていたのでありがたい。ダウンロードしたアプレットを斜め読みするに、ニュートン法かなにかで解いている様子だったけど細かいところまでは追えていない。亜音速側の解がうまく得られなかったため、グラフにはスロート以降の $M>1$ の解だけをプロットしている。

(\frac{A}{A^*})^2=\frac{1}{M^2}\{\frac{2}{\gamma+1}(1+\frac{\gamma-1}{2})M^2\}^{(\gamma+1)/(\gamma-1)}

おわりに

準1次元ノズルフローをシミュレーションで解いて、解析解に一致するところまでを確認した。次回は計算条件を変えて実行するなどやってみたい。

[1]	John D. Anderson, "Computational Fluid Dynamics: The Basics With Applications," McGraw-Hill Inc. (1995)

[2]	ここでは段階、階層の意か。なお本文でのつづりはeschelonとなっている

monotonica Engimono Notebook and more