monotonica Engimono Notebook and more

FORmula-TRANslation Translation into Julia (1)

FORTRANをJuliaに翻訳します。その1

  1. はじめに
  2. Incompressible Couette Flow
  3. ソースコードのかきなおし
  4. おわりに

はじめに

Interaxion Podcastのep.24をきっかけに教えてもらったJulia in Physics 2021という研究会を追っていたら、FortranからJuliaを始めたい人向けの講演を見つけた。JuliaConと同様に講演アーカイブ動画が残っていてありがたい。

講演動画と併せて同じ著者によるFortranから始めるJuliaというウェブサイトも公開されている。 サイト内で辿れるFortranのコードをJuliaへ移植してみるのページにある移植事例を参考に、手持ちのいにしえのFORTRANコードをJuliaに翻訳してみた。

Incompressible Couette Flow

手頃なFORTRANコードを探すのに少し苦労したけど、とある古文書を紐解いて一つ見繕うことができた。

本書第9章では非圧縮性流体のクエット流れを取り扱っている。 クエット流れは厳密解の存在する粘性流れ。 ウィキペディアによれば巽流体力学にも記述があるらしいけど、僕はまだ読んだ記憶がない気がする。 クエット流れの壁面水平方向速度 u u はナビエ・ストークス方程式から得られる以下の式で表される。

∂2u∂y2=0 \dfrac{\partial^2 u}{\partial y^2} = 0

この式は実質的には2階常微分方程式なので、積分すればたやすく解を得ることができて、速度 u u は壁からの距離に応じた直線分布となる。

u=c1y+c2 u = c_1y+c_2

この速度分布を得るいにしえのFORTRANコードは本書Appendix Aに掲載されている。 Appendixの章題にもある通り、三重対角行列を解くアルゴリズムはThomas algorithmとして知られていて、このアルゴリズムを使った解法になる。 行数にして全部で63行しかないし、そんなに大変な作業ではないだろう……と高をくくっていたら、Juliaの文法をだいぶ忘れてしまっていて案外手こずった。 本当はもう少し複雑なコードを翻訳しようと思っていたけど、このレベルから始めて良かった。

ソースコードのかきなおし

基本的には前述したFortranのコードをJuliaへ移植してみるのページ、特に終わりにあるチェックリストに沿って変更していけば問題ない。 例えば以下に示すメインループ部分（一部省略）について、変更前のFORTRANのコードと、変更後のJuliaのコードをそれぞれ示す。

DO5 KK=1,KKEND
C     SET ORIGINAL COEFFICIENTS
      DO2 J=2,N
      Y(J)=Y(J-1)+DEL
      A(J)=AA
      IF(J.EQ.N) A(J)=0.0
      （...中略...）
C     UPPER BIDIAGONAL FORM
      DO3 J=3,N
      D(J)=D(J)-B(J)*A(J-1)/D(J-1)
      C(J)=C(J)-C(J-1)*B(J)/D(J-1)
3     CONTINUE
      （...中略...）
      TEST=MOD(KK,KKMOD)
      IF(TEST.GT.0.01) GO TO 5
      WRITE(6,100) KK,TIME,DELTIM
      WRITE(*,100) KK,TIME,DELTIM
      WRITE(6,101)
      WRITE(*,101)
      WRITE(6,102) (J,Y(J),U(J),B(J),D(J),A(J),C(J),J=1,NN)
      WRITE(*,102) (J,Y(J),U(J),B(J),D(J),A(J),C(J),J=1,NN)
5     CONTINUE
John David Anderson, "Computational Fluid Dynamics: The Basics With Applications," McGraw-Hill Inc. (1995), p.538. 
for KK=1:KKEND
    # SET ORIGINAL COEFFICIENTS
    for J=2:N
        Y[J]=Y[J-1]+DEL
        A[J]=AA
        if J==N
            A[J]=0.0
        end
    （...中略...）
    # UPPER BIDIAGONAL FORM
    for J=3:N
        D[J]=D[J]-B[J]*A[J-1]/D[J-1]
        C[J]=C[J]-C[J-1]*B[J]/D[J-1]
    end
    （...中略...）
    TEST=KK%KKMOD
    if TEST<0.01
        println("SOLUTION AT     KK=  $KK     TIME= $TIME     DELTIM= $DELTIM")
        println("")
        println("   J      Y         U         B         D         A         C")
        for J=1:NN
            @printf "%2i %10.3e %10.3e %10.3e %10.3e %10.3e %10.3e\n" J Y[J] U[J] B[J] D[J] A[J] C[J]
        end
    end
end

主なポイントと気付き事項は以下。

  • 前述のウェブサイトで示されている通り、累乗は^、余り計算は%に置き換え

  • 配列の添字は丸括弧()から角括弧[]に修正する。演算中の丸括弧を含めないよう、適当な添字入りでの一括置換を何度か繰り返せばOK

  • DOをforに直すのはいいとして、IFをif（小文字表記）に修正しないといけないのは盲点だった。

  • if文は1行で書くのをやめてendで閉じる必要がある。

  • 出力のformattingに少し苦労した。printlnでは見た目よく揃えるのが難しそうだったので、ここではPrintfパッケージを使った。（参考）

    • using Printfからの@printfで出力。桁数はお好みで

    • いにしえのフォーマッティングe10.3は10.3eに、i2は2iになる。いま試したらzero paddingのi2.2→2.2iもいける。

    • 文字列はアルファベットが変わってa10→10sとする。

    • そして先頭にパーセント%をつけるのを忘れない：%10.3e, %2i, %2.2i

  • いろいろと試行錯誤するのにJuliaでコンパイルが不要になるのは本当に楽。

ソースコードを実行するとKKENDで指定した回数だけ反復計算がなされ、その過程ではKKMODで指定した間隔で出力がなされる。 今回の計算は一瞬で終わってしまい、FORTRANとJuliaでの実行速度の比較はできなかった。

FORTRANとJuliaの両者で出力は概ね一致することを確認している。 このご時世に単精度演算とする意味はないと思って、Juliaへの翻訳時に倍精度演算に直していることから、誤差の丸めに影響が出ている。 有効桁数の観点からは表示桁数ももう少し増やしても問題ない。

反復回数による速度分布の変化をグラフに示した。縦軸に速度、横軸に壁からの距離を取っている。100ステップではまだ収束が甘く、200ステップ回せばほぼ直線分布が得られる。 パラメータを変更すればステップ数をもう少し削れるかもしれない。

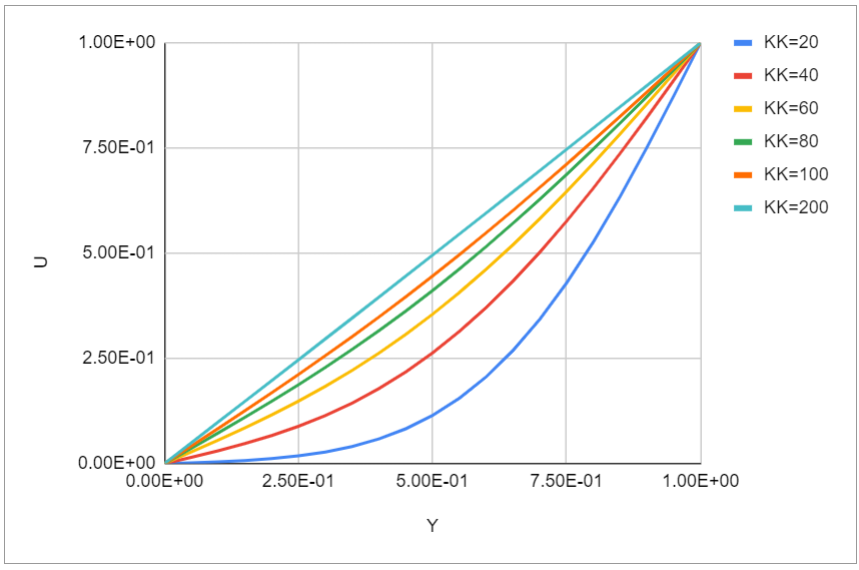
u-profile

グラフはJuliaのPlotsパッケージで書ければ良かったのだけれど、今はそのやり方すらも忘れていた。 文法でいえば、1年前に少し触ったはずのJuliaの文法はほとんど忘れていた一方で、数年単位で書いていないはずのFortranの文法はちゃんと覚えていて、これが母国語か……となった。

おわりに

手持ちのいにしえのFORTRANコードを練習がてらJuliaに翻訳した。 これを取っ掛かりにしてもう少しJuliaっぽいコードを扱えるようになれると良い。

© hinagata. Last modified: March 16, 2023. Website built with Franklin.jl and the Julia programming language. 免責事項